For the last six or eight months, off and on, I’ve been trying to write some code that will create a Voronoi diagram from a set of random points, inspired by Amit Patel’s Polygonal Map Generation demo. In the last week or so, I had a bit of a break-through, in that I finally managed to get an implementation of Fortune’s Algorithm put together that would actually work and generate the Voronoi edges and vertices correctly so that I could render them. Since most of the existing implementations I’ve been trying to work from are either broken or an enormous pain in the ass to try to understand, I’m planning on writing up my implementation, once I’m finally happy with it. I’ve still got a fair way to go, since right now I’m only outputting the graph edges and vertices successfully, and while that renders prettily, I haven’t gotten to the point that I have all of the really useful graph connectivity information being output yet. Hopefully, if everything goes well, I’ll manage to finish that up by the end of the week, but this has proven to be a real bugger of a problem to solve.
As I mentioned, most of the implementations I’ve studied are either incomplete or broken. Particularly, I haven’t found an example yet that correctly clips the edges of the generated Voronoi polygons to a rectangular area. So long as all you care about is rendering the graph to the screen, this isn’t a big problem, since most 2D graphics libraries will happily draw lines that extend beyond the drawable area of the screen. However, if you’re trying to subdivide a rectangular region into Voronoi polygons, its kind of nice to have your edges actually clipped to that region. What I’m envisioning doing with this code eventually is using it to render 3D maps, subdivided into territories, but with an overlaid rectangular grid for moving units – think of the strategic map in Total War games or Lords of the Realm.
After I got frustrated with trying to make the broken clipping code I was working from perform correctly, I trolled Google and came across the Cohen-Sutherland line-clipping algorithm. This looked to be exactly what I needed, and wonder of wonders, the Wikipedia page actually featured a readable, reasonable example, rather than the obtuse academic pseudo-code you usually find there (see the Fortune’s Algorithm article…). The only thing I would caution you about with the Wikipedia example is that it uses a coordinate system where the origin is the lower-left bounds of a rectangle as usually encountered in mathematics, rather than the upper-left origin we commonly use in computer graphics, so some tweaking is necessary.
The code for this example can be downloaded from my github repository, at https://github.com/ericrrichards/dx11.git. The algorithm is included in the Algorithms project, while the example code is in the CohenSutherlandExample project. The example code is a quick-and-dirty mess of GDI drawing code, so I’m going to focus on the algorithm code.
After clipping:
NOTE: I apologize if this looks all screwed up, with extra line breaks. Blogger is terrible and loves to mangle the html I try to post up with Windows Live Writer. I’m looking at moving off it for something else soon.
The Cohen-Sutherland Algorithm
The Cohen-Sutherland algorithm relies on the insight that we can divide a 2D rectilinear space containing the clipping region into nine different regions, where the center region is our clipping region. Using bit-wise operations, we can classify these nine regions using a 4-bit bitvector. For readability, I’m using an enum with the [Flags] attribute, but using an unsigned byte would work equally well. These values are often referred to as outcodes.
[Flags]
enum OutCode {
Inside = 0,
Left = 1,
Right = 2,
Bottom = 4,
Top = 8
}
You can see how these outcode values are used to classify the space in the screenshots above. Since they are bitwise flags, we can represent the top left region as Top|Left = 0x9, for instance.
With our outcodes defined, it is simple to classify a given endpoint of a line segment and determine its position relative to the clipping rectangle by comparing the X and Y coordinates of the point against the bounds of the rectangle.
private static OutCode ComputeOutCode(float x, float y, RectangleF r) {
var code = OutCode.Inside;
if (x < r.Left) code |= OutCode.Left;
if (x > r.Right) code |= OutCode.Right;
if (y < r.Top) code |= OutCode.Top;
if (y > r.Bottom) code |= OutCode.Bottom;
return code;
}
Note that the conditions testing the Y coordinate are flipped compared to the Wikipedia example – WinForms and most other graphics libraries define the origin of their coordinate systems in the top-left corner of the screen, rather than the bottom right as is common in mathematics.
For convenience, I’ve also provided an overload of this method that takes a System.Drawing.PointF, rather than the separate X and Y coordinates.
private static OutCode ComputeOutCode(PointF p, RectangleF r) { return ComputeOutCode(p.X, p.Y, r); }
Clipping Lines
After classifying the endpoints of the line, there are three cases to consider when clipping the line.
- (Trivial) Both endpoints are within the clipping rectangle. In this case, we do not need to clip the line at all.
- (Trivial) Both endpoints are in the same region outside the clipping region – i.e. both endpoints are within one of the 8 regions surrounding the clipping region, or the endpoints are in different regions, but the line will not cross the clipping region. For instance, this would apply to a line entirely within the Top|Left region, and also to a line with one endpoint in the Top|Left region and one in the Top|Right region. We can discard these lines without clipping.
- The line crosses the clipping region, either because one endpoint is within the clipping region, or the endpoints do not share a region code – i.e. a line between Left and Right, or Top|Left and Right. We will need to clip one or both of the endpoints to the clipping region.
Here you can see the three cases illustrated:
| Case: | |
| 1 – Trivial Accept |  |
| 2 – Trivial Reject |  |
| 3 – Clip one or both endpoints | 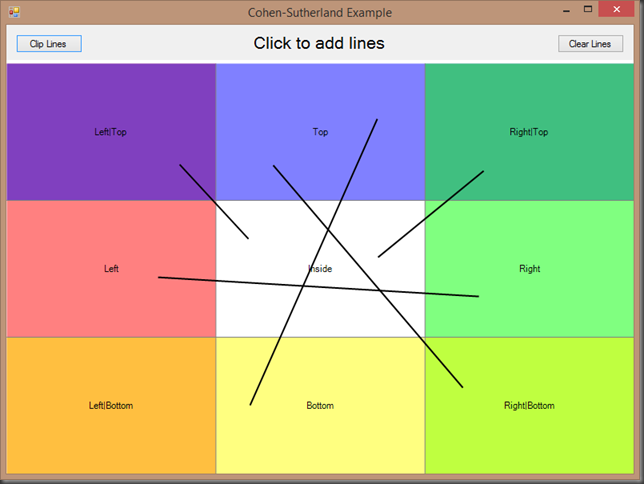 |
Clipping an Endpoint to the Rectangle
To calculate the intersection of the line with the clipping rectangle, we will use the point-slope form of the equation for a line. Below is the derivation of the formula that we will use for calculating clipping against the left and right edges of the clipping rectangle.
To clip against the top and bottom of the clipping rectangle, we cannot use this formula directly. In the case of a vertical line, we will end up with a slope that is undefined. So, we have to something a little tricky. If we pretend that we are using a coordinate system that is rotated 90 degrees, and swap our x and y coordinates appropriately, the same formula works for clipping against the top and bottom edges of the clipping rectangle.
private static PointF CalculateIntersection(RectangleF r, PointF p1, PointF p2, OutCode clipTo) {
var dx = (p2.X - p1.X);
var dy = (p2.Y - p1.Y);
var slopeY = dx / dy; // slope to use for possibly-vertical lines
var slopeX = dy / dx; // slope to use for possibly-horizontal lines
if (clipTo.HasFlag(OutCode.Top)) {
return new PointF(
p1.X + slopeY * (r.Top - p1.Y),
r.Top
);
}
if (clipTo.HasFlag(OutCode.Bottom)) {
return new PointF(
p1.X + slopeY * (r.Bottom - p1.Y),
r.Bottom
);
}
if (clipTo.HasFlag(OutCode.Right)) {
return new PointF(
r.Right,
p1.Y + slopeX * (r.Right - p1.X)
);
}
if (clipTo.HasFlag(OutCode.Left)) {
return new PointF(
r.Left,
p1.Y + slopeX * (r.Left - p1.X)
);
}
throw new ArgumentOutOfRangeException("clipTo = " + clipTo);
}
Full algorithm
I was initially going to have this return the custom LineSegment object that I’m using in my Voronoi map code, but decided on using a more general Tuple<> instead.
public static Tuple<PointF, PointF> ClipSegment(RectangleF r, PointF p1, PointF p2) {
// classify the endpoints of the line
var outCodeP1 = ComputeOutCode(p1, r);
var outCodeP2 = ComputeOutCode(p2, r);
var accept = false;
while (true) { // should only iterate twice, at most
// Case 1:
// both endpoints are within the clipping region
if ((outCodeP1 | outCodeP2) == OutCode.Inside) {
accept = true;
break;
}
// Case 2:
// both endpoints share an excluded region, impossible for a line between them to be within the clipping region
if ((outCodeP1 & outCodeP2) != 0) {
break;
}
// Case 3:
// The endpoints are in different regions, and the segment is partially within the clipping rectangle
// Select one of the endpoints outside the clipping rectangle
var outCode = outCodeP1 != OutCode.Inside ? outCodeP1 : outCodeP2;
// calculate the intersection of the line with the clipping rectangle
var p = CalculateIntersection(r, p1, p2, outCode);
// update the point after clipping and recalculate outcode
if (outCode == outCodeP1) {
p1 = p;
outCodeP1 = ComputeOutCode(p1, r);
} else {
p2 = p;
outCodeP2 = ComputeOutCode(p2, r);
}
}
// if clipping area contained a portion of the line
if (accept) {
return new Tuple<PointF, PointF>(p1, p2);
}
// the line did not intersect the clipping area
return null;
}
Next Time…
Hopefully I make some progress on my Voronoi maps code. It looks pretty cool, but it’s not terribly useful except as eye candy until I get the connections between the generated polygons generated.



No comments :
Post a Comment